This article is based on Machine Learning in Action , published on February 2011. It is being reproduced here by permission from Manning Publications. Manning publishes MEAP (Manning Early Access Program,) eBooks and pBooks. MEAPs are sold exclusively through Manning.com. All pBook purchases include free PDF, mobi and epub. When mobile formats become available all customers will be contacted and upgraded. Visit Manning.com for more information. [ Use promotional code ‘java40beat’ and get 40% discount on eBooks and pBooks ]
also read:
- Java Tutorials
- Java EE Tutorials
- Design Patterns Tutorials
- Java File IO Tutorials
Introduction
Gradient Ascent uses the whole dataset on each update. This is fine with 100 examples but, with billions of data points containing thousands of features, it is unnecessarily expensive in terms of computational resources. An alternative to this method is to update the weights using only one instance at a time. This is known as Stochastic Gradient Ascent. Stochastic Gradient Ascent is an example of an on-line learning algorithm. This is known as on-line because we can incrementally update the classifier as new data comes in rather than all at once. The all-at-once method is known as batch processing.
Pseudocode for the Stochastic Gradient Ascent would look like:
Start with the weights all set to 1 For each piece of data in the dataset: Calculate the gradient of one piece of data Update the weights vector by alpha*gradient Return the weights vector
The following listing contains the Stochastic Gradient Ascent algorithm.
Listing 1 Stochastic Gradient Ascent
def stocGradAscent0(dataMatrix, classLabels): m,n = shape(dataMatrix) alpha = 0.01 weights = ones(n) for i in range(m): h = sigmoid(sum(dataMatrix[i]*weights)) error = classLabels[i] - h weights = weights + alpha * error * dataMatrix[i] return weights
Stochastic Gradient Ascent is very similar to Gradient Ascent except that the variables h and error are now single values rather than vectors. There also is no matrix conversion so all of the variables are NumPy arrays.
To try this out, enter the code from listing 1 into logRegres.py and enter the following in your Python shell:
>>> reload(logRegres) <module 'logRegres' from 'logRegres.py'> >>> dataArr,labelMat=logRegres.loadDataSet() >>> weights=logRegres.stocGradAscent0(array(dataArr),labelMat) >>> logRegres.plotBestFit(weights)
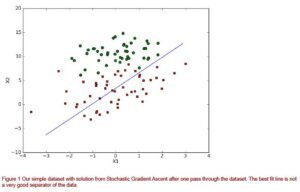
After executing the code to plot the best-fit line, you should see something similar to figure 1. The resulting best fit line is ok but certainly not great. If we were to use this as our classifier, we would misclassify one-third of the results.
 One way to look at how good the optimization algorithm is doing is to see if it is converging. That is, are the parameters reaching a steady value or are they constantly changing? I have taken the Stochastic Gradient Ascent algorithm in listing 1 and modified it to run through the dataset 200 times. The weights were then plotted in figure 2.
One way to look at how good the optimization algorithm is doing is to see if it is converging. That is, are the parameters reaching a steady value or are they constantly changing? I have taken the Stochastic Gradient Ascent algorithm in listing 1 and modified it to run through the dataset 200 times. The weights were then plotted in figure 2.
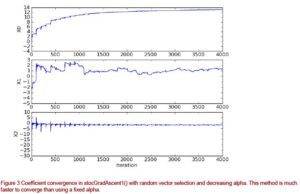 Figure 2 shows how the weights change in our simple Stochastic Gradient Ascent algorithm over 200 iterations of the algorithm. Weight 2, labeled X2 in figure 2, takes only 50 cycles to reach a steady value, but weights 1 and 0 take much longer. An additional item to notice from this plot is that there are small periodic variations, even though the large variation has stopped. If you think about what is happening, it should be obvious that there are pieces of data that don’t classify correctly and cause a large change in the weights. We would like to see the algorithm converge to a single value rather than oscillate, and we would like to see the weights converge more quickly.
Figure 2 shows how the weights change in our simple Stochastic Gradient Ascent algorithm over 200 iterations of the algorithm. Weight 2, labeled X2 in figure 2, takes only 50 cycles to reach a steady value, but weights 1 and 0 take much longer. An additional item to notice from this plot is that there are small periodic variations, even though the large variation has stopped. If you think about what is happening, it should be obvious that there are pieces of data that don’t classify correctly and cause a large change in the weights. We would like to see the algorithm converge to a single value rather than oscillate, and we would like to see the weights converge more quickly.
The Stochastic Gradient Ascent algorithm of listing 1 has been modified to address the problems shown in figure 2, and this is given in listing 2.
Listing 2 Modified Stochastic Gradient Ascent
def stocGradAscent1(dataMatrix, classLabels, numIter=150): m,n = shape(dataMatrix) weights = ones(n) for j in range(numIter): dataIndex = range(m) for i in range(m): alpha = 4/(1.0+j+i)+0.01 #1 randIndex = int(random.uniform(0,len(dataIndex)))#2 h = sigmoid(sum(dataMatrix[randIndex]*weights)) error = classLabels[randIndex] - h weights = weights + alpha * error * dataMatrix[randIndex] del(dataIndex[randIndex]) return weights #1 Alpha changes with each iteration #2 Update vectors are randomly selected
The code in listing 2 is similar to that of listing 1. However, two things have been added to improve it.
The first thing to note is in #1 alpha changes on each iteration. This will improve the oscillations that occur in the dataset seen in figure 2 or high-frequency oscillations. Alpha decreases as the number of iterations increases. However, it never reaches 0 because there is a constant term in #1. We need to do this so that, after a large number of cycles, new data still has some impact. Perhaps you are dealing with something that is changing with time. Then, you may want to let the constant term be larger to give more weight to new values. The second thing about the decreasing alpha function is that it decreases by 1/(j+i); j is the index of the number of times we go through the dataset, and i is the index of the example in the training set. This gives an alpha that is not strictly decreasing when j<<max(i). The avoidance of a strictly decreasing weight is shown to work in other optimization algorithms, such as simulated annealing as well.
The second improvement in listing 1 appears in #2. Here, we are randomly selecting each instance to use in updating the weights. This will reduce periodic variations that we saw in figure 2.
An optional argument to the function has also been added. If no third argument is given, then 150 iterations will be done. However, if a third argument is given, that will override the default.
If you compare figures 2 and 3, you will notice two things. The first thing you may notice is that the coefficients in figure 3 do not show the regular motion as those in figure 2. This is due to the random vector selection of stocGradAscent1(). The second thing you will notice is that the horizontal axis is much smaller in figure 3 than in figure 2. This is because with stocGradAscent1() we can converge on weights much quicker. Here, we use only 20 passes through the dataset.
Let’s see this code in action. After you have entered the code from listing 2 to logRegres.py, enter the following in your Python shell:
>>> reload(logRegres) <module 'logRegres' from 'logRegres.py'> >>> dataArr,labelMat=logRegres.loadDataSet() >>> weights=logRegres.stocGradAscent1(array(dataArr),labelMat) >>> logRegres.plotBestFit(weights)
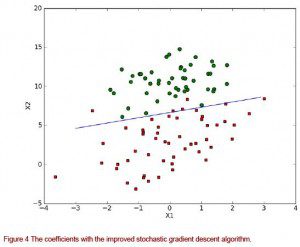
You should see a plot similar to that in figure 4. The results are very similar to that of GradientAscent() but far fewer calculations are involved.
 The default number of iterations is 150, but you can change this by adding a third argument to stocGradAscent1() like:
The default number of iterations is 150, but you can change this by adding a third argument to stocGradAscent1() like:
>>> weights=logRegres.stocGradAscent1(array(dataArr),labelMat, 500)
Summary
In this article, we learned about Stochastic Gradient Ascent and how to make modifications to yield better results.

