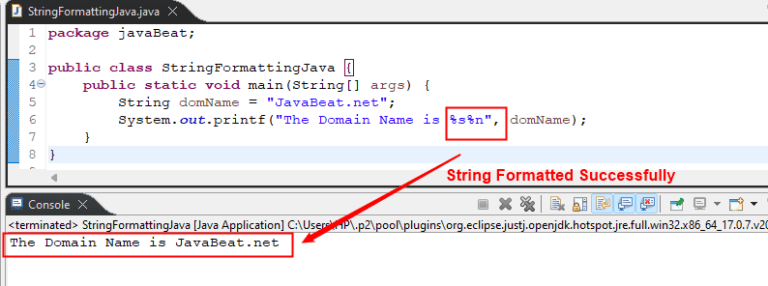
To format a string with printf() in Java, execute the “System.out.printf()” statement with the “%s” or “%S” format specifier.
Java
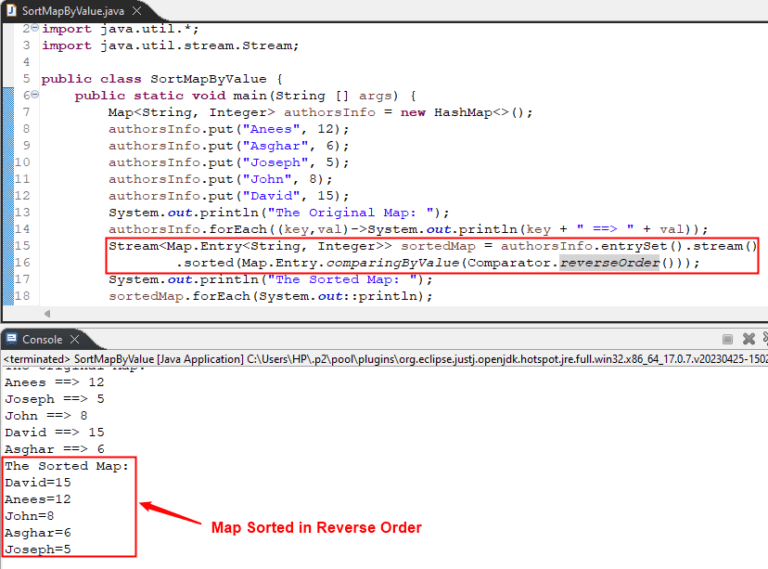
How to Sort a Map by Value in Java
In Java, you can sort a map by value using three methods: “Collections.sort()”, “Stream().sorted()”, and “Custom Comparators”.
How to Use StringUtils Class in Java
To Use the StringUtils class in Java, add its corresponding Apache Commons dependency in a “pom.xml” file of your maven project.
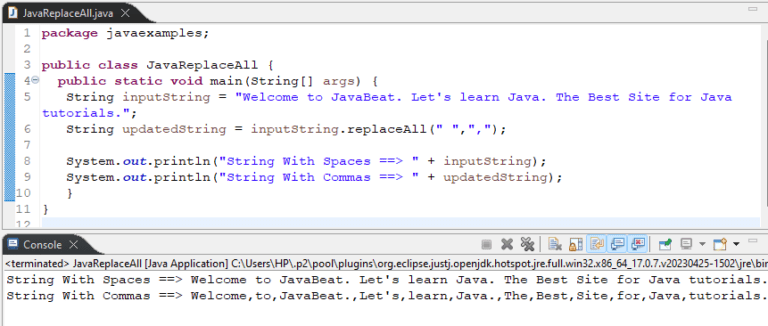
How to Use String.replaceAll() Method in Java
The “String.replaceAll()” method is used to replace all occurrences of a specific character, word, or substring, with a new character, word, or substring.
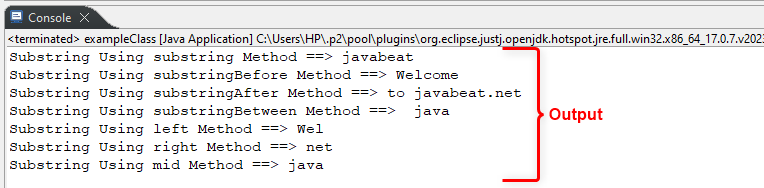
How to Use String substring() Method in Java
To use the String substring() method in Java, follow the syntax “inputString.substring(int startIndex);” or “inputStr.substring(int startIndex, int endIndex);”.
How to Use Set contains() Method in Java
In Java, the set contains() method accepts the target element as a parameter and is used with a dot syntax: “setName.contains(Object targetElement);”.
How to Get the Current Working Directory in Java
To get the current directory in Java, you can use the classes like “System”, “Paths”, “File”, “FileSystems” and “SystemUtils”.
How to Use a Swap() Method in Java?
The Collections.swap() method interchanges the two values at the given index within the List or collection of the object as shown in this article.